1,無次元数
レイノルズ数
![]()
マッハ数・・・圧縮性流体に関するパラメータ
![]()
2,流れの種類
2,1種類
流線:任意の時刻tにおいて流れの中に1本の空間曲線をとり曲線状の各点における速度ベクトル![]() が曲線の接線になるときその曲線を流線という.
が曲線の接線になるときその曲線を流線という.
→Euler的
流跡線:一つの流体粒子が時間とともに移動する軌跡を考えこれを流跡線という.
流脈線:点![]() を時々刻々に通過したすべての流体粒子の位置を連ねた曲線.
を時々刻々に通過したすべての流体粒子の位置を連ねた曲線.
Ex)煙・染料
→Lagrange的
2,2流れを可視化する
空気の流れの可視化の例:流れ中に細い糸や軽いテープなどを数多く取り付け,それらの挙動を観察する(これをタフト法という).
水の流れの可視化の例:流れの中にインクなどのトレーサーを流す(これをトレーサー法あるいは色素注入法という).
3,流体の性質
流体に作用する力は流体の変形速度に比例する.
◎粘性係数![]()
![]()
3,1流体要素の変形→テンソル表示
![]()
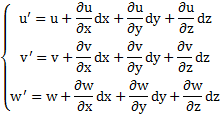
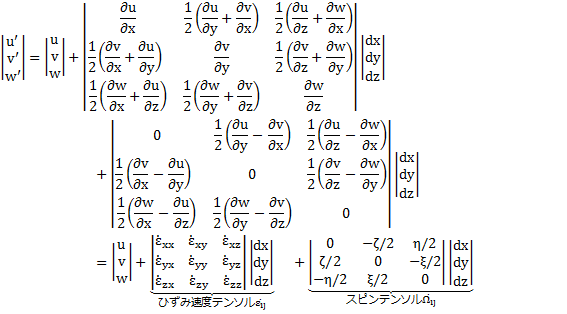
3,2ひずみ速度テンソル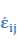
対角成分:ひずみ速度(単位時間あたりのひずみ)
非対角成分:せん断変形
3,3スピンテンソル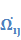
![]() はそれぞれ
はそれぞれ![]() 軸周りの剛体的回転運動を表す.
軸周りの剛体的回転運動を表す.
3,4渦度
![]()
とすると渦度ωは
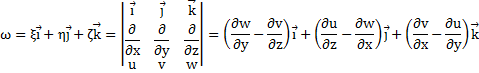
で表される.
◎基本としては![]() を覚える.
を覚える.
3,5粘性応力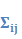 :これはひずみ速度に依存
:これはひずみ速度に依存
![]()
※Aは係数を表す
![]()
※μは粘性係数
※λは第二粘性係数
以上をまとめて変形(詳しくは2.9〜を参考に)
![]()
よって
![]()
![]()
![]()
運動している流体の圧力を求める
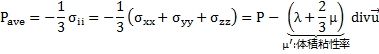
Stocksの仮説
![]()
これを用いて上式を整理すると
![]()
書く成分は下の通り
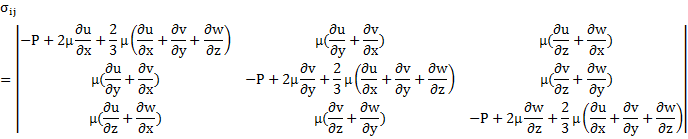
ここで非圧縮性流体の場合
![]()
より
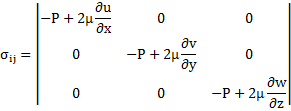
となる.
4,加速度・運動方程式など
4,1空間加速度
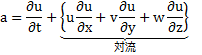
4,2運動方程式
![]()
![]()
関する運動方程式
![]()
両辺からdV消去
![]()
4,3仕事からポテンシャル
◎静止流体
外力
![]()
とする
このとき仕事は
![]()
![]()
ここでポテンシャルdUは
![]()
ただしUが存在する条件は![]()
またこのとき![]() をみたし,これを保存場という.
をみたし,これを保存場という.
また中心圧力をPとすると![]() が成立することから
が成立することから![]() が成り立つ
が成り立つ
5,層流と乱流
Re=2300くらいが境目
5,1円環の管摩擦係数
![]()
さらに層流では・・・
![]()
5,2粘性流体

◎主流
・速度勾配=0
・非粘性流れ
◎境界層内
・速度勾配大
・粘性応力
・Re数とともに境界層は薄くなる
◎層流境界層から乱流境界層へ
・乱流遷移点

◎乱流境界層
・運動量拡散が大きく流速が一様化
・粘性応力と乱流応力
◎境界層流れ
・抗力 低速時―1乗
高速時―2乗
5,3流体抵抗とは?
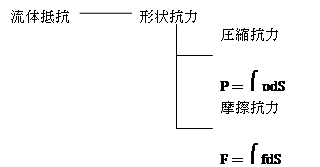
5,4流線型
◎流れを物体表面から剥離させないことで圧力抗力を低減させる
特徴
・流れ方向への投影面積が小さい(抗力小,揚力大)
・流れが剥離しない
|
|
|
|
|
圧力抗力≪摩擦抗力 |
|
圧力抗力≪摩擦抗力 |
6,次元解析Buckinghamのπ定理
6,1基本
ある物理現象を支配する物理量の数が![]() のn個であり,次式の関数関係があるとする.
のn個であり,次式の関数関係があるとする.
![]()
このとき,![]() を表すのにk個の基本単位が必要であるとすると,この物理現象は(n-k)個の無次元パラメータを用いて次式で表せる.
を表すのにk個の基本単位が必要であるとすると,この物理現象は(n-k)個の無次元パラメータを用いて次式で表せる.
![]()
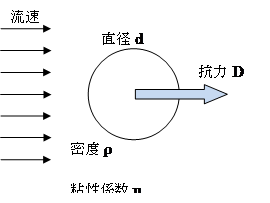
6,2(例)一様流中に設置された球に作用する抗力
|
|
この現象に関係する物理量として,次の5つを選ぶ.
基本単位(次元)は,長さ[L],重さ[M],時間[T]の3つであるから,バッキンガムのΠ定理によれば,2つの無次元パラメータが得られる. |
• 基本単位(次元)と同数の基本物理量を選ぶ.ここでは,代表寸法である直径d,代表速度である流速Vおよび密度ρを選ぶ(基本物理量の選び方は原則として任意).
• 基本物理量に選ばなかった抗力D,粘性係数μを,各々基本物理量と組み合わせて,無次元パラメータ![]() を作る.
を作る.
![]()
![]()
• 式(4.7)の,![]() が無次元となるようにα,β,γを決定する.
が無次元となるようにα,β,γを決定する.
![]()
![]()
![]()
![]()
![]()
![]()
• バッキンガムのΠ定理より,次式を得る.
![]()
• 一般に,球が流体から受ける抗力Dを評価する際には,抗力係数![]() が用いられる.
が用いられる.
![]()
• 式(4.13),式(4.14)より次の関係が得られる.
![]()
![]()
抗力係数は,レイノルズ数Reのみの関数となる.
7,保存則
7,1質量保存則
検査体積を以後CVで表す
7,1,1一般的な質量保存則式
![]()
ただし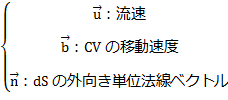
7,1,2CVを空間に固定すると仮定
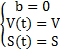
仮定した式を書き直す
![]()
第二項に注目.
これは面から出て行く分が![]() で面に入る分が
で面に入る分が![]() であることを示す.
であることを示す.
→入る質量と出る質量が等しい.
![]()
7,1,3質量バランス式の適用例
◎仮定
(1)定常流れ:各位置での流れは時間的に変化しない.
(2)準一次元流れ:検査体積の両端断面で流れは一様とし,流速は各々の断面平均値で表して差し支えない.
(3)断面![]() ,
,![]() で流れの速度勾配は無視できる.
で流れの速度勾配は無視できる.
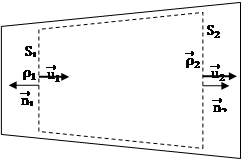
以上から準一次元定常流れの質量バランス式が導出
![]()
7,2連続方程式
7,2,1導出
7,1,3で仮定した式においてCVが空間に固定されている体積とすると
![]()
と書ける.
また左辺第二項にガウスの発散定理を用いると
![]()
となる.以上から次式が導ける.
![]()
![]()
7,2,2 3つの仮定
(1)(x,y,z)直交座標のとき
![]()
(2)定常流れのとき
![]()
(3)非圧縮性のとき
![]()
7,3運動量バランス
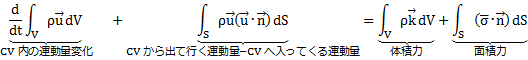
7,4運動方程式
![]()
7,4,1導出
運動量バランス式に対してCVが空間に固定されている体積とすると
![]()
と書ける.
また左辺第二項にガウスの発散定理を用いると
![]()
右辺第二項にガウスの発散定理を用いると
![]()
となる.以上から次式が導ける.
![]()
Vは任意にとることができるので次式を満たすことが必要十分条件.
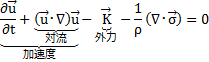
よって運動方程式が導けた.
7,4,2 Eulerの運動方程式:非粘性流体の場合
応力テンソルが対角成分のみとなるから次のようにかける.
![]()
7,4,3Navier-Stokes 方程式:粘性流体の場合
Stocksの定理より
![]()
とかける.(3,5参照)
非圧縮性かつ粘性係数μが一定のとき上式を代入すると
![]()